Menjelajahi Dunia Bangun Datar Gabungan: Contoh Soal Tematik untuk Siswa SD Kelas 4 yang Menyenangkan dan Mudah Dipahami
Pendahuluan: Mengapa Bangun Datar Penting dalam Kehidupan Sehari-hari?
Matematika seringkali dianggap sebagai pelajaran yang rumit oleh sebagian siswa. Namun, jika diajarkan dengan cara yang menyenangkan dan relevan dengan kehidupan sehari-hari, matematika bisa menjadi sangat menarik. Salah satu cabang matematika yang paling dekat dengan realitas kita adalah geometri, khususnya bangun datar. Sejak duduk di bangku sekolah dasar, kita sudah mulai diperkenalkan dengan berbagai bentuk bangun datar seperti persegi, persegi panjang, segitiga, hingga lingkaran.
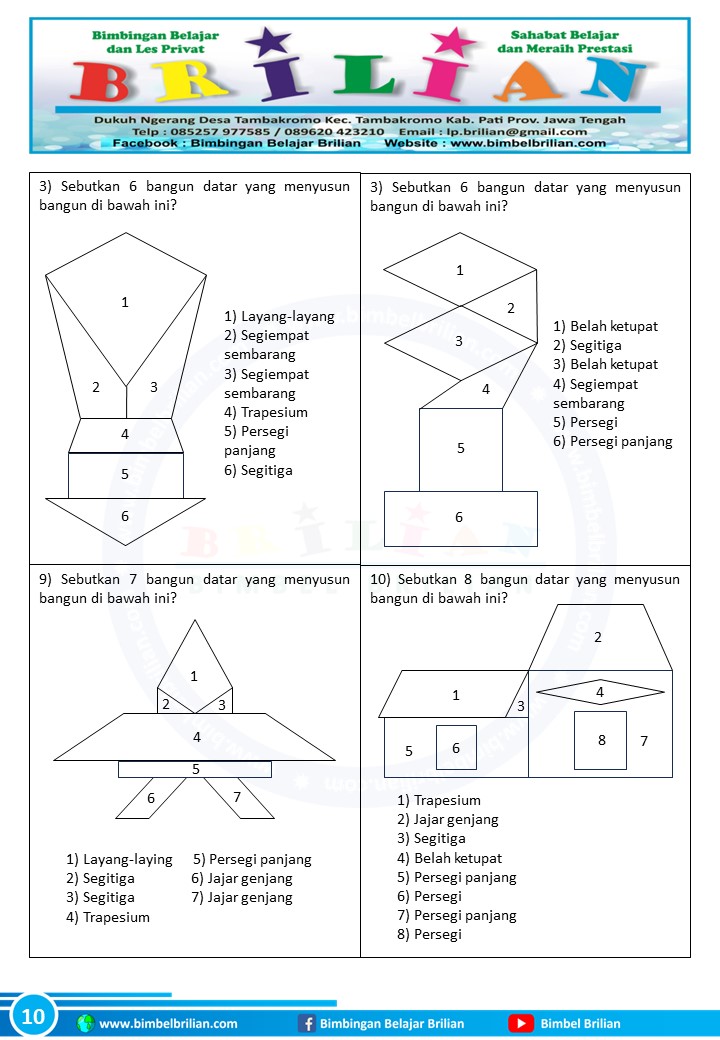
Di kelas 4 SD, pemahaman tentang bangun datar akan diperdalam, termasuk bagaimana menghitung keliling dan luasnya. Namun, tantangan yang lebih menarik muncul ketika kita bertemu dengan "bangun datar gabungan". Apa itu bangun datar gabungan? Sesuai namanya, ini adalah bentuk yang terbentuk dari penggabungan dua atau lebih bangun datar sederhana. Misalnya, sebuah rumah bisa digambarkan sebagai gabungan persegi panjang (dinding) dan segitiga (atap), atau sebuah lapangan bermain anak yang berbentuk L.
Artikel ini akan membahas secara tuntas konsep bangun datar gabungan untuk siswa kelas 4 SD. Kita akan mulai dengan mengingat kembali konsep dasar bangun datar sederhana, kemudian memahami apa itu bangun datar gabungan, dan yang terpenting, bagaimana menyelesaikan soal-soalnya dengan pendekatan "tematik". Pendekatan tematik berarti kita akan belajar melalui contoh-contoh soal yang relevan dengan kehidupan sehari-hari dan seringkali melibatkan lebih dari satu mata pelajaran, membuat pembelajaran menjadi lebih bermakna dan tidak membosankan.
Mengingat Kembali Konsep Dasar Bangun Datar Sederhana
Sebelum melangkah ke bangun datar gabungan, mari kita segarkan ingatan tentang beberapa bangun datar dasar yang sering kita jumpai:
-
Persegi
- Ciri-ciri: Memiliki empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat).
- Keliling (K): Jumlah panjang semua sisi. Jika ‘s’ adalah panjang sisi, maka K = 4 × s.
- Luas (L): Hasil kali sisi dengan sisi. L = s × s = s².
-
Persegi Panjang
- Ciri-ciri: Memiliki empat sisi, dengan dua pasang sisi yang berhadapan sama panjang, dan empat sudut siku-siku.
- Keliling (K): Jumlah panjang semua sisi. Jika ‘p’ adalah panjang dan ‘l’ adalah lebar, maka K = 2 × (p + l).
- Luas (L): Hasil kali panjang dengan lebar. L = p × l.
-
Segitiga
- Ciri-ciri: Memiliki tiga sisi dan tiga sudut. Ada berbagai jenis segitiga (sama sisi, sama kaki, siku-siku, sembarang).
- Keliling (K): Jumlah panjang ketiga sisinya. K = sisi1 + sisi2 + sisi3.
- Luas (L): Setengah dari hasil kali alas dengan tinggi. L = ½ × alas × tinggi.
-
Lingkaran
- Ciri-ciri: Bangun datar yang semua titiknya berjarak sama dari titik pusat.
- Keliling (K): Jarak mengelilingi tepi lingkaran. K = π × d (pi kali diameter) atau K = 2 × π × r (2 kali pi kali jari-jari). Nilai π (pi) biasanya 3,14 atau 22/7.
- Luas (L): Daerah yang dilingkupi lingkaran. L = π × r² (pi kali jari-jari kuadrat).
Memahami rumus-rumus ini adalah kunci utama untuk menyelesaikan soal bangun datar gabungan, karena kita akan "memecah" bangun datar gabungan menjadi bangun-bangun datar sederhana ini.
Apa Itu Bangun Datar Gabungan dan Bagaimana Menghitungnya?
Bangun datar gabungan adalah bentuk yang terbentuk dari kombinasi dua atau lebih bangun datar sederhana. Misalnya, gabungan sebuah persegi dan sebuah segitiga, atau sebuah persegi panjang dan setengah lingkaran.
Strategi Umum untuk Menghitung Bangun Datar Gabungan:
- Identifikasi Bangun Datar Pembentuk: Langkah pertama adalah melihat bangun gabungan tersebut, kemudian memisahkannya menjadi bangun-bangun datar sederhana yang sudah kita kenal (persegi, persegi panjang, segitiga, lingkaran). Terkadang kita perlu menggambar garis bantu untuk mempermudah pemisahan ini.
- Tentukan Dimensi yang Diketahui dan yang Perlu Dicari: Perhatikan ukuran-ukuran yang sudah diberikan pada soal (panjang, lebar, sisi, alas, tinggi, jari-jari). Jika ada ukuran yang belum diketahui tetapi penting untuk perhitungan, coba cari tahu dari informasi lain yang tersedia.
- Hitung Luas Masing-masing Bangun Datar: Setelah terpisah, hitunglah luas setiap bangun datar sederhana menggunakan rumus yang sesuai.
- Jumlahkan Luas untuk Mendapatkan Luas Total: Luas bangun datar gabungan adalah total penjumlahan luas dari semua bangun datar sederhana pembentuknya.
- Hitung Keliling dengan Hati-hati: Ini adalah bagian yang seringkali membingungkan. Keliling bangun datar gabungan adalah total panjang sisi-sisi terluar bangun tersebut. Artinya, sisi-sisi yang "berimpit" atau berada di dalam gabungan TIDAK DIHITUNG sebagai keliling. Bayangkan Anda sedang berjalan mengelilingi tepi luar bentuk tersebut.
Pendekatan Tematik dalam Pembelajaran Bangun Datar Gabungan
Pendekatan tematik berarti kita belajar dengan mengaitkan materi pelajaran ke dalam tema atau topik yang lebih luas dan relevan dengan kehidupan siswa. Dalam konteks bangun datar gabungan, ini berarti soal-soal tidak hanya berupa gambar abstrak, tetapi disajikan dalam bentuk cerita atau situasi nyata.
Manfaat Pendekatan Tematik:
- Relevansi: Siswa melihat langsung bagaimana matematika digunakan dalam kehidupan sehari-hari, misalnya dalam merancang taman, membuat denah rumah, atau menghitung bahan yang dibutuhkan.
- Motivasi: Pembelajaran menjadi lebih menarik dan bermakna karena siswa bisa membayangkan skenario yang diceritakan.
- Pemecahan Masalah: Siswa diajak untuk berpikir kritis dan menerapkan konsep matematika untuk menyelesaikan masalah nyata.
- Integrasi Mata Pelajaran: Seringkali soal tematik melibatkan keterampilan membaca (memahami cerita soal), bahkan bisa dihubungkan dengan seni (desain) atau ilmu pengetahuan alam (misalnya, menghitung luas area tanam).
Contoh Soal Bangun Datar Gabungan (dengan Pembahasan Lengkap)
Mari kita langsung ke contoh soal. Ingat, gambar adalah kunci. Bayangkan bentuknya atau gambar di kertas Anda!
Contoh Soal 1: Taman Depan Rumah
Bayangkan sebuah taman depan rumah Pak Budi. Taman tersebut terdiri dari dua bagian: bagian depan berbentuk persegi panjang dan bagian belakang yang menempel berbentuk persegi.
- Bagian persegi panjang memiliki panjang 8 meter dan lebar 5 meter.
- Bagian persegi memiliki sisi yang berimpit dengan lebar persegi panjang, sehingga panjang sisi perseginya adalah 5 meter.
Soal:
a. Berapakah luas total taman Pak Budi?
b. Berapakah keliling taman Pak Budi yang akan dipasang pagar?
Pembahasan:
Langkah 1: Identifikasi Bangun Datar Pembentuk
- Bangun 1: Persegi Panjang
- Bangun 2: Persegi
Langkah 2: Tentukan Dimensi
- Persegi Panjang: Panjang (p) = 8 m, Lebar (l) = 5 m
- Persegi: Sisi (s) = 5 m (karena berimpit dengan lebar persegi panjang)
Langkah 3: Hitung Luas Masing-masing Bangun Datar
- Luas Persegi Panjang (L1):
- L1 = p × l
- L1 = 8 m × 5 m
- L1 = 40 m²
- Luas Persegi (L2):
- L2 = s × s
- L2 = 5 m × 5 m
- L2 = 25 m²
Langkah 4: Jumlahkan Luas untuk Mendapatkan Luas Total
- Luas Total Taman (L_total):
- L_total = L1 + L2
- L_total = 40 m² + 25 m²
- L_total = 65 m²
Langkah 5: Hitung Keliling dengan Hati-hati
Ingat, keliling adalah panjang sisi-sisi terluar. Sisi yang berimpit (panjang 5m di tengah) tidak dihitung.
-
Sisi-sisi terluar taman adalah:
- Panjang persegi panjang: 8 m
- Lebar persegi panjang yang tidak berimpit: 5 m
- Panjang sisi persegi yang tidak berimpit: 5 m
- Panjang sisi persegi yang tidak berimpit lainnya: 5 m
- Panjang sisa sisi persegi panjang (ini adalah sisi yang sejajar dengan sisi persegi yang berimpit, dan sama panjang dengan sisi persegi): 5 m
- Panjang sisi persegi panjang yang di bagian atas: 8 m
-
Keliling Total Taman (K_total):
- K_total = 8 m (atas) + 5 m (kanan persegi panjang) + 5 m (bawah persegi) + 5 m (kiri persegi) + 5 m (sisa lebar persegi panjang) + 8 m (bawah persegi panjang)
- K_total = 8 + 5 + 5 + 5 + 5 + 8
- K_total = 36 m
Jawaban:
a. Luas total taman Pak Budi adalah 65 m².
b. Keliling taman Pak Budi yang akan dipasang pagar adalah 36 m.
Contoh Soal 2: Desain Kolam Ikan Berbentuk L
Bayu sedang membantu ayahnya mendesain kolam ikan. Kolam tersebut memiliki bentuk seperti huruf "L". Kita bisa membaginya menjadi dua persegi panjang.
- Bagian horizontal (tidur) memiliki panjang 10 meter dan lebar 4 meter.
- Bagian vertikal (berdiri) memiliki panjang 6 meter dan lebar 3 meter.
- Kedua bagian ini berimpit.
Soal:
a. Berapa luas dasar kolam ikan tersebut?
b. Jika keliling kolam akan dipasangi batu hias, berapa panjang batu yang dibutuhkan?
Pembahasan:
Langkah 1: Identifikasi Bangun Datar Pembentuk (dengan garis bantu)
Kita bisa membayangkan dua cara membagi bentuk L:
- Cara 1: Dua persegi panjang.
- Persegi Panjang 1 (P1): yang besar, misalnya panjang 10m, lebar 4m.
- Persegi Panjang 2 (P2): yang kecil, "menempel" di salah satu sisi P1. Jika P1 panjang 10m dan lebar 4m, maka P2 memiliki panjang 6m dan lebar 3m. (Perhatikan bahwa panjang P2 6m itu adalah total panjang ke atas, dan lebarnya 3m).
- Cara 2 (Metode Pengurangan): Sebuah persegi panjang besar yang "dilubangi" di sudutnya.
- Misal, bangun besar adalah persegi panjang dengan panjang (10m) dan tinggi (4m + 6m = 10m).
- Lalu, ada lubang berbentuk persegi panjang di sudutnya.
- Kita akan gunakan Cara 1 karena lebih mudah untuk siswa kelas 4.
Langkah 2: Tentukan Dimensi
- Persegi Panjang 1 (P1 – bagian bawah): Panjang (p1) = 10 m, Lebar (l1) = 4 m
- Persegi Panjang 2 (P2 – bagian atas yang menempel): Panjang (p2) = 6 m, Lebar (l2) = 3 m
Langkah 3: Hitung Luas Masing-masing Bangun Datar
- Luas P1 (L1):
- L1 = p1 × l1 = 10 m × 4 m = 40 m²
- Luas P2 (L2):
- L2 = p2 × l2 = 6 m × 3 m = 18 m²
Langkah 4: Jumlahkan Luas untuk Mendapatkan Luas Total
- Luas Total Kolam (L_total):
- L_total = L1 + L2
- L_total = 40 m² + 18 m²
- L_total = 58 m²
Langkah 5: Hitung Keliling dengan Hati-hati
Ini bagian yang tricky untuk bentuk L. Kita harus mengidentifikasi semua sisi terluar.
-
Sisi-sisi terluar:
- Sisi panjang P1: 10 m
- Sisi lebar P1 (yang tidak berimpit): 4 m
- Sisi panjang P2: 6 m
- Sisi lebar P2: 3 m
- Sisi sisa dari panjang P1 (setelah P2 menempel): 10 m – 3 m = 7 m
- Sisi sisa dari lebar P1 (setelah P2 menempel): 6 m – 4 m = 2 m (ini sisi yang menghubungkan bagian P1 dan P2)
- Sisi yang pendek di pojok dalam: ini adalah sisa dari lebar P1 setelah dikurangi lebar P2. Karena P1 lebarnya 4m dan P2 menempel dengan lebar 3m, maka sisa lebar P1 di bagian atas adalah 4m – 3m = 1m.
-
Keliling Total Kolam (K_total):
- K_total = 10 m (panjang P1) + 4 m (lebar P1) + 7 m (sisa panjang P1) + 1 m (sisa lebar P1) + 3 m (lebar P2) + 6 m (panjang P2)
- K_total = 10 + 4 + 7 + 1 + 3 + 6
- K_total = 31 m
Jawaban:
a. Luas dasar kolam ikan adalah 58 m².
b. Panjang batu hias yang dibutuhkan adalah 31 m.
Contoh Soal 3: Plang Nama Toko (Persegi Panjang dan Setengah Lingkaran)
Sebuah toko kue membuat plang nama baru. Plang tersebut berbentuk persegi panjang di bagian bawah dan setengah lingkaran di bagian atasnya.
- Bagian persegi panjang memiliki panjang 140 cm dan lebar 70 cm.
- Bagian setengah lingkaran menempel pada sisi panjang persegi panjang (140 cm).
Soal:
a. Berapa luas permukaan plang nama tersebut?
b. Berapa panjang bingkai yang dibutuhkan untuk mengelilingi tepi plang nama tersebut? (Gunakan π = 22/7)
Pembahasan:
Langkah 1: Identifikasi Bangun Datar Pembentuk
- Bangun 1: Persegi Panjang
- Bangun 2: Setengah Lingkaran
Langkah 2: Tentukan Dimensi
- Persegi Panjang: Panjang (p) = 140 cm, Lebar (l) = 70 cm
- Setengah Lingkaran: Diameter (d) = 140 cm (karena menempel pada sisi panjang persegi panjang).
- Maka, jari-jari (r) = d / 2 = 140 cm / 2 = 70 cm.
Langkah 3: Hitung Luas Masing-masing Bangun Datar
- Luas Persegi Panjang (L1):
- L1 = p × l = 140 cm × 70 cm = 9.800 cm²
- Luas Setengah Lingkaran (L2):
- Luas lingkaran penuh = π × r²
- L2 = ½ × π × r²
- L2 = ½ × (22/7) × 70 cm × 70 cm
- L2 = ½ × 22 × (70/7) × 70
- L2 = ½ × 22 × 10 × 70
- L2 = 11 × 700
- L2 = 7.700 cm²
Langkah 4: Jumlahkan Luas untuk Mendapatkan Luas Total
- Luas Total Plang (L_total):
- L_total = L1 + L2
- L_total = 9.800 cm² + 7.700 cm²
- L_total = 17.500 cm²
Langkah 5: Hitung Keliling dengan Hati-hati
Keliling adalah panjang sisi terluar. Sisi panjang persegi panjang yang berimpit dengan diameter setengah lingkaran TIDAK DIHITUNG.
-
Sisi-sisi terluar plang adalah:
- Dua sisi lebar persegi panjang: 70 cm + 70 cm
- Satu sisi panjang persegi panjang (bagian bawah): 140 cm
- Keliling busur setengah lingkaran: ½ × Keliling lingkaran penuh
- Keliling lingkaran penuh = π × d = (22/7) × 140 cm = 22 × (140/7) = 22 × 20 = 440 cm
- Keliling busur = ½ × 440 cm = 220 cm
-
Keliling Total Plang (K_total):
- K_total = 70 cm (kiri) + 140 cm (bawah) + 70 cm (kanan) + 220 cm (busur atas)
- K_total = 70 + 140 + 70 + 220
- K_total = 500 cm
Jawaban:
a. Luas permukaan plang nama tersebut adalah 17.500 cm².
b. Panjang bingkai yang dibutuhkan adalah 500 cm.
Contoh Soal 4: Denah Kamar Tidur (Persegi Panjang dengan Sudut Dipotong Segitiga)
Seorang arsitek membuat denah kamar tidur. Bentuknya hampir persegi panjang, tetapi salah satu sudutnya dipotong membentuk segitiga siku-siku karena ada lemari sudut.
- Ukuran kamar tidur yang berbentuk persegi panjang adalah panjang 7 meter dan lebar 5 meter.
- Sudut yang dipotong membentuk segitiga siku-siku. Panjang salah satu sisi siku-sikunya adalah 2 meter (berimpit dengan panjang kamar) dan sisi siku-siku lainnya adalah 3 meter (berimpit dengan lebar kamar).
Soal:
a. Berapa luas lantai kamar tidur tersebut?
b. Berapa panjang lis lantai yang dibutuhkan untuk mengelilingi kamar?
Pembahasan:
Langkah 1: Identifikasi Bangun Datar Pembentuk (Metode Pengurangan)
- Kita bisa melihat ini sebagai sebuah persegi panjang besar yang "dikurangi" atau "dipotong" oleh sebuah segitiga siku-siku.
- Bangun 1: Persegi Panjang
- Bangun 2: Segitiga Siku-siku (yang dipotong)
Langkah 2: Tentukan Dimensi
- Persegi Panjang: Panjang (p) = 7 m, Lebar (l) = 5 m
- Segitiga Siku-siku: Alas (a) = 2 m, Tinggi (t) = 3 m.
- Sisi miring segitiga (sisi potong) perlu dihitung jika untuk keliling. Menggunakan teorema Pythagoras (mungkin terlalu maju untuk kelas 4, jadi kita bisa sederhanakan soalnya agar sisi miringnya langsung diketahui atau kita abaikan jika soalnya hanya minta keliling sisi yang lurus). Untuk kelas 4, biasanya sisi miring diberikan atau dihindari. Mari kita asumsikan sisi miringnya sudah diketahui jika perlu, atau kita akan fokus pada keliling yang lebih sederhana. Untuk latihan ini, kita akan anggap siswa bisa menghitung sisi miring jika diberikan nilai sederhana, atau kita akan langsung berikan nilainya. Mari kita asumsikan sisi miring adalah 3.6 m (akar dari 2^2 + 3^2 = 4+9=13, akar 13 sekitar 3.6).
Langkah 3: Hitung Luas Masing-masing Bangun Datar
- Luas Persegi Panjang (L1):
- L1 = p × l = 7 m × 5 m = 35 m²
- Luas Segitiga Siku-siku (L2):
- L2 = ½ × alas × tinggi = ½ × 2 m × 3 m = 3 m²
Langkah 4: Kurangkan Luas untuk Mendapatkan Luas Total
- Luas Total Kamar (L_total):
- L_total = L1 – L2
- L_total = 35 m² – 3 m²
- L_total = 32 m²
Langkah 5: Hitung Keliling dengan Hati-hati
Keliling adalah panjang sisi-sisi terluar. Sisi yang dipotong (sisi segitiga yang berimpit dengan sisi persegi panjang) TIDAK DIHITUNG. Sisi miring segitiga yang menjadi bagian dari batas luar DIHITUNG.
-
Sisi-sisi terluar kamar:
- Panjang kamar: 7 m
- Lebar kamar: 5 m
- Sisa panjang kamar setelah dipotong: 7 m – 2 m = 5 m
- Sisa lebar kamar setelah dipotong: 5 m – 3 m = 2 m
- Sisi miring segitiga (sisi potong): 3.6 m (ini nilai yang diasumsikan)
-
Keliling Total Kamar (K_total):
- K_total = 7 m (panjang penuh) + 5 m (lebar penuh) + 5 m (sisa panjang) + 2 m (sisa lebar) + 3.6 m (sisi miring)
- K_total = 7 + 5 + 5 + 2 + 3.6
- K_total = 22.6 m
Jawaban:
a. Luas lantai kamar tidur tersebut adalah 32 m².
b. Panjang lis lantai yang dibutuhkan adalah 22.6 m.
Tips dan Trik untuk Memahami Bangun Datar Gabungan
- Gambar Itu Penting! Selalu coba gambar bentuk bangun datar gabungan tersebut. Jika sudah ada gambar, coba tambahkan garis bantu untuk memisahkannya.
- Pecah Menjadi Bagian Kecil: Ini adalah kunci utamanya. Jangan panik melihat bentuk yang aneh. Pikirkan, "Bentuk apa saja yang bisa saya temukan di sini?"
- Fokus pada Dimensi: Perhatikan baik-baik angka yang diberikan. Apakah itu panjang, lebar, sisi, alas, tinggi, atau jari-jari? Apakah ada dimensi yang perlu Anda hitung terlebih dahulu?
- Hati-hati dengan Keliling: Ini adalah jebakan paling umum. Ingat, keliling HANYA menghitung sisi-sisi terluar. Sisi yang berada di dalam bangun gabungan (garis potong atau garis impit) tidak dihitung. Bayangkan Anda "berjalan" mengelilingi tepiannya.
- Periksa Satuan: Pastikan Anda menggunakan satuan yang konsisten (misalnya, semua dalam meter atau semua dalam sentimeter) dan tulis satuan pada jawaban akhir (misalnya m², cm, dll.).
- Latihan Terus-menerus: Semakin banyak Anda berlatih, semakin terbiasa Anda mengidentifikasi bangun datar sederhana dalam bentuk gabungan dan menghitungnya dengan benar.
- Hubungkan dengan Dunia Nyata: Carilah contoh bangun datar gabungan di sekitar Anda: jendela, meja, kolam renang, lapangan olahraga, potongan kue, dan lain-lain. Ini akan membuat belajar lebih menyenangkan.
Kesimpulan
Mempelajari bangun datar gabungan mungkin terlihat menantang pada awalnya, namun dengan pemahaman konsep dasar yang kuat dan strategi pemecahan masalah yang tepat, siswa SD kelas 4 pasti bisa menguasainya. Pendekatan tematik yang mengaitkan materi dengan kehidupan sehari-hari bukan hanya membuat matematika lebih relevan dan menarik, tetapi juga membantu siswa mengembangkan keterampilan berpikir kritis dan memecahkan masalah.
Ingatlah bahwa kunci untuk sukses adalah memecah masalah besar menjadi bagian-bagian yang lebih kecil dan mudah dikelola. Dengan latihan yang konsisten dan sikap yang positif, setiap siswa dapat menjelajahi dunia geometri dengan percaya diri dan menemukan keindahan matematika dalam berbagai bentuk di sekitar kita. Mari terus belajar dan berkreasi dengan bangun datar!